
Conversión del numero 37 a un numero binario.
Dividimos el 37 entre 2 y lo que nos quedade residuo es 1 y el cociente es 18, después ahora vamos a dividir el 18 entre dos.
Lo que nos queda de residuo es 0 y el cociente es 9.Ahora vamos a dividir el 9 entre dos.
Lo que nos queda de residuo es 1 y el coiciente es 4.Ahora vamos a dividie el 4 entre 2.
Lo que nos queda de residuo es 0 y el coeficiente es 2.Ahora vamos a dividir el 2 entre 2.
Lo que nos queda de residuo es 0 y el coeiciente es 1 .Ahora por ultimo dividimos el 1 entre dos.
Como el 1 entre 2 no cabe lo que nos queda de residuo es 1 y el coeficiente será 0.
Ahora para el número binario que nos queda serán los residuos de todas las divisiones que hicimos y aclarando que para acomodar el numero binario es de el ultimo residuo al primero
El numero binario queda así:
100101
Otra forma es con la tablita de las diapositivas de la Dra. Elisa, es más rápido, recordando que el numero binario lo checaremos de atrás para delante y la tablita de abajo para arriba.
Bueno ya convertimos de el numero decimal que teníamos que era el 37 a numero binario.
Ahora empezamos la ejecución de la maquina turing, de acuerdo a las instrucciones que la venían en el examen, escanee la tablita del examen para que fuera más fácil la visualización.
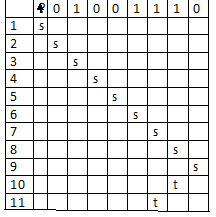
Aquí está la ejecución
Y aquí es como nos queda la ejecución
Lo que hacemos es de acuerdo a las instrucciones
“S” inicia, se moverá hacia la derecha y lo que va a imprimir es un 0
“S” ve un 1, lo imprime y continúa hacia la derecha.
“S” ve un 0, lo imprime y continua hacia la derecha.
“S” ve un 0, lo imprime y continua hacia la derecha.
“S” ve un 1, lo imprime y continúa hacia la derecha.
“S” ve un 0, lo imprime y continua hacia la derecha
“S” ve un 1, lo imprime y continúa hacia la derecha.
“S” ve el vacio ahora imprimirá un 0 y se moverá hacia la izquierda cave decir que cambia su estado de s a t.
“t” ve un 1, lo imprime y se mueve hacia la izquierda , después “t” ve un 0 y ahí se para cambiando el 0 por un 1 .
La salida de la maquina turing en binario
01001110
Para convetirlo a decimal:
La salida de la maquina tu ring es el 78 en decimal
¿Que hace la maquina?
En este caso analizando lo que hace es multiplicar el número por 2 y sumarle 4.
¿cual es la complejidad en términos de computación y memoria?
Como nos podemos dar cuenta en la tablita de ejecución realizo 11 traslaciones las enumere cada traslación para que fuera más fácil su visualización.
Cualquier cosa que no entienda el porqué lo hice así, solo déjeme el comentario y yo les respondo o si algo hice mal solo háganmelo saber para volverlo a analizar y hacer la ejecución.














No hay comentarios:
Publicar un comentario